关系
关系(relation) 与生活中的关系别无二致,就是一个东西和另一个东西的关系(废话
但是为了表示这种东西,数学家又要用某些符号系统来表示
序偶(有序对)
序偶(ordered couple) 啊就是两个有序排列的东西,比如$x$和$y$的排列方式就有$<x,y>$和$<y,x>$两种
像坐标就是一个序偶
那如果我们要表示很多可能相近的关系又该怎么办呢,总不能写一大堆吧
如果有两个集合 $A$ 和 $B$ ,我想要一大堆(全部)从$A$中元素到$B$中元素的关系要怎么样呢
$A \times B$ 表示 $A$ 和 $B$ 的笛卡尔积,就是一个包含了很多 $<x,y>$ 的集合, $x$ 属于 $A$ 而 $y$ 属于 $B$
那什么是关系呢
如果一个集合里面全都是序偶,那这个集合就是一个二元关系,被记作$R$
如果呢 $<x,y> \in R$ ,那 $x$ 和 $y$ 以 $R$ 相关,写作 $xRy$
如果 $R \subseteq A \times B$ ,那 $R$ 就是 $A$ 到 $B$ 的一个关系,如果 $A$ 就是 $B$ , $B$ 就是 $A$ ,那 $R$ 就是 $A$ 上的关系
| $\varnothing$ 是任意集合上的空关系, $E_A=A \times A$ 是 $A$ 上的全域关系,$I_A={ <x,x> | x \in A }$叫$A$上的恒等关系 |
如果说有个关系$R$,那它的所有序偶的第一个元素的集合叫它的定义域或者前域,和初中学的是一个东西,记作$dom~R$,当然也有值域或者后域,记作$ran~R$,还有个$fld~R = dom~ ~R \cup ran~ ~R$叫做$R$的域(field)
我们的关系又该如何表示?
最最数学的方法就是用集合来表示啦,也就是在某个集合里面塞上一堆序偶
或者也可以用图,更准确地说是有向图来表示,对一个$<x,y>$,只需要画一条从$x$到$y$的有向线段就好啦
亦可以用关系矩阵,和那个表示图的邻接矩阵是一样的,非常简单
关系有什么性质呢
有的关系有特殊的性质,这些性质很多时候是比较好使的
某个关系有自反性指这个集合上的所有元素都和自己有这个关系,比如说在${1,2,3}$上的关系$R_1 = { <1,1>,<2,2>,<3,3> }$就是有自反性的,而$R_2 = { <1,1>,<2,2> }$就不是;相反,如果每个元素都和自己没这个关系,那这个关系就有反自反性
而对称性是指一个关系里面每个$<x,y>$都有对应的$<y,x>$;反对称性则是指关系里除了$<x,x>$这种自己对自己的序偶之外都不对称
传递性是说一个关系里如果有$<x,y>,<y,z>$,那也一定有$<x,z>$,传递性好像反不了(
很容易发现 $=$ 是满足上面三个关系的哎
关系当然是可以运算的
作为一种集合,关系当然可以进行集合的所有运算,除此之外当然还有些别的
复合运算(就像复合函数一样)
就像$f \circ g=g(f(x))$一样,$R \circ S$表示类似的概念,具体懒得写出来了,反正是一样的(
逆运算
顾名思义,逆运算就是把原本关系的所有序偶给反向,比如有个关系$R={ <1,2>,<3,4> }$那它的逆就是$R^{-1}={<2,1>,<4,3>}$,非常的简单
显然有$(R \circ S)^{-1} = S^{-1}\circ R^{-1}$
幂运算
| 专家定义在$A$上的关系$R$有$R^0={<x,x> | x \in A}$,对任何$n\geq 1$有$R^n = R^{n-1} \circ R$ |
对于有限集$A$上面的关系$R$,存在自然数 $t,s$ 使 $R^t=R^s$
这是因为无论幂运算几次,其中的元素都是在$A\times A$里面的,而$A\times A$的子集是有限的,于是在不限制$n$的情况下必然会有$R^t=R^s$撞车
闭包运算
啥是闭包运算呢说实话都不知道为啥要叫闭包,就是说在某个集合$A$上的某个关系$R$没有某个关系应该有的性质,然后又能找到一个最小的有这个性质的$R’$符合$R\subseteq R’$,那这个$R’$就叫做$R$的某某闭包
也就是 $R$ 的有某个性质的最小超集
$R$的自反闭包记作$r(R)$,对称闭包记作$s(R)$,传递闭包记作$t(R)$
| 显然 $\displaystyle r(R)=R \cup I_A,~s(R)=R\cap R^{-1},~t(R)=\bigcup^{\infty}_{i=1}R^i,~若 | A | =n,~t(R)=\bigcup^{n}_{i=1}R^i$ |
还有一些乱七八糟的性质
\[\begin{aligned} rs(R)=sr(R) \\ rt(R)=tr(R) \\ st(R)\subseteq ts(R) \end{aligned}\] \[\begin{aligned} r(R_1)\cup r(R_2) = r(R_1\cup R_2) \\ s(R_1)\cup s(R_2) = s(R_1\cup R_2) \\ t(R_1)\cup t(R_2) \subseteq t(R_1\cup R_2) \end{aligned}\]有什么关系是特殊的呢
当然是有的,像是等价关系、相容关系和偏序关系是三类有特殊性质的关系,且等价关系$\subseteq$相容关系
等价关系
等价关系可以用来表示等价(废话),只需要一个关系具有自反性、对称性和传递性就行
模 $n$ 同余关系就是一种等价关系,记作$x\equiv y \pmod n$也就是
x % n == y % n # 显然 x 和 y 和 n 必须是自然数
如果一个集合 $A$ 有个等价关系 $R$ ,又有个 $x$ 在这个 $R$ 关系里面,那 $A$ 里所有和 $x$ 等价的元素可以组成一个集合 $[x]_R$ ,这个集合叫做 $x$ 关于 $R$ 的等价类, $x$ 叫做这个等价类的生成元或者代表元
如果把由 $R$ 所决定的所有等价类又都放到一个集合里面,那这个新的集合叫做 $A$ 关于 $R$ 的商集,记作 $A/R$
举个栗子: $A={ 1,2,3,4,5,6,7,8 }$, $R$ 是 $x\equiv y \pmod 3$ ,那么
\[A/R=\{ \{ 1,4,7 \},\{2,5,8\},\{3,6\} \}\]非常的简单
对于某个集合 $A$,如果把它拆成一些元素不遗漏不重复的非空子集,那这些集合组成的集合叫做 $A$ 的一个划分,里面的那些子集叫做划分的块或类,显然上面的 $A/R$ 就是一个划分,这些称为商集的划分又叫 $R$ 导出的等价划分
通过某个划分, 可以通过下面这样导出它对应的等价关系
\[R=(S_1\times S_1) \cup (S_2 \times S_2)\cup \cdots \cup (S_m \times S_m)\]只要一个关系具有自反性和对称性,那这个关系就是相容关系,但是这玩意确实没啥可以讲的,基本都和等价关系差不多
偏序关系
偏序关系可以表示集合里面每个元素之间的单向关系,如果 $A$ 上面的关系 $R$ 有自反性、反对称性和传递性,那这个关系就是偏序关系,对 $<x,y> \in R$ 可以记作 $x \leq y$ 。这个 $A$ 由于上面有偏序关系,就可以被叫做偏序集,写作 $<A,\leq>$
由于这关系是有单向顺序的,所以专家发明了一种直观的表示这种关系的图,叫哈斯图(Hasse)(但是并不是他发明的
比如要表示 $A={ 1,2,3,4,6,12 }$ 上面的整除关系就可以画出这样一个图
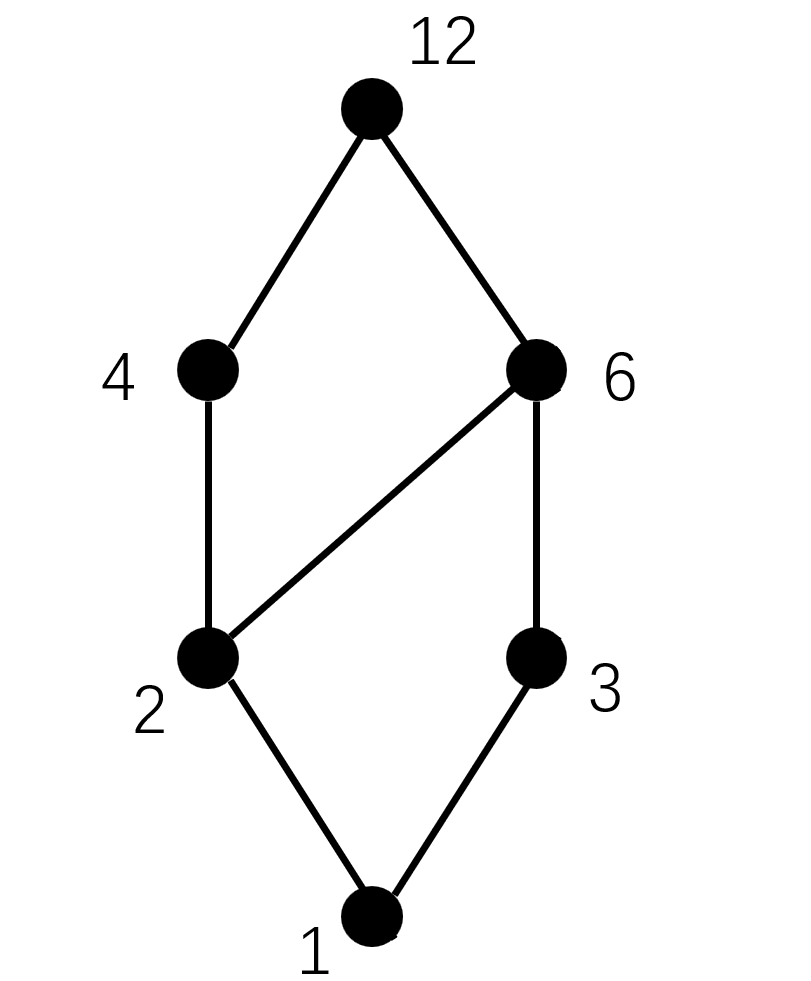
(用PPT画的,非常丑陋
可以发现我们要让“最小”的元素排在下面,然后按大小一层一层往上排(也就是 $<x,y>$ 里面越 $x$ 的元素就越在下面)
[!tip] 哈斯图一定一定要竖着画!!!
类似于函数啥的,专家又给出了一些新的定义
在哈斯图里面,如果一个元素在所有其他元素的下面,那这个元素就叫做这个图里面的最小元素或最小元,同样的还有最大元素或最大元
如果一个元素只是在最下面(下面没有更多元素了),那就像函数的极小值一样叫做极小元素或极小元,同理还有极大元素和极大元(显然最某元一定是极某元
对 $<A,\leq>$ 和 $A$ 和 $A$ 的子集 $B$ ,如果 $a \in A$ 对 $\forall x \in B$ 有 $x \leq a$ 的话,$a$ 就是 $B$ 的上界,反之亦有下界
[!tip] $a$ 不一定属于 $B$ !
如果 $a$ 是最小的上界的话,那它还会叫做最小上界或上确界,当然也有最大下界或下确界
如果有 $<A,\leq>$ , $A$ 里面每两个元素都有关系,那它的哈斯图就是一条线,这个偏序关系叫做全序关系或者线序关系, $<A,\leq>$ 叫做全序集或者线序集或者链
如果有 $<A,\leq>$ , $A$ 的每个非空子集都有最小元素,那这个偏序关系叫做良序关系, $<A,\leq>$ 叫做良序集
终于结束了,好累(
贵圈真乱(
函数
显而易见函数也是一种关系呐,但是我已经不想重复函数的定义了
如果函数 $f$ 的定义域是 $A$ ,值域是 $B$ ,有一种新的记法是 $\text{dom } f = A$ , $\text{ran } f = B$
好像只要记住跟高数书一样的概念就好了,关于单射和满射
单射就是 $x$ 和 $y$ 一对一,满射就是每个 $x$ 和 $y$ 都有对应关系,双射则是既单射又满射
然后可以用 $\circ$ 来表示函数的复合运算,就和上面说的一样, $f \circ g$ 就是 $g(f(x))$
至于逆函数啥的……应该个个都会吧(